Quadratic Formula Calculator

This quadratic formula calculator solves quadratic equations of the form ax² + bx + c = 0 and shows the solving process using the quadratic formula. To use the calculator, please provide values for a, b, and c, then click the "Solve" button.

Quadratic equations

A quadratic equation is a second-degree algebraic expression that can be written in the form,

ax² + bx + c = 0

where x represents an unknown, a, b, and c are constants, and a≠0; this is because if a = 0, there will be no second-degree term, and the equation will therefore not be quadratic. Being a "second-degree algebraic expression" means that the highest order variable term in the equation must have an order of 2, and that this term must exist. In other words, to be a quadratic equation, the expression must include an x² term, and cannot include a higher order term such as x³, x⁷, etc.

Quadratic equations can take on a number of different forms; the form above is referred to as the standard form of a quadratic equation. As long as an expression can be re-written such that it takes on the form above, it is a quadratic equation, even if it is not originally in standard form.

Solving quadratic equations:

There are a number of different methods for solving a quadratic equation, such as computing the square root, factoring, completing the square, using the quadratic formula, or graphing the equation. Deciding which method to use is a large part of solving quadratic equations because depending on the specific quadratic equation, certain methods may be easier or more efficient to use.

Computing a square root:

Computing a square root of a quadratic equation that is a perfect square is arguably the simplest way to solve a quadratic equation. However, it is only possible in a very limited number of cases where the quadratic equation involves perfect squares. For example:

x² = 1

x = ±1

The above is a solution to a very simple quadratic equation. There are other types of quadratic equations that can be solved in this way, such as:

(x + 1)² = 2

x + 1 = ±√2

x = √2 - 1   or   x = -√2 - 1

In many cases however, we will not have a perfect square, and this method of solving quadratic equations cannot be used.

Graphing a quadratic equation:

Graphing a quadratic equation is another way to easily solve the equation, assuming that you have access to a graphing calculator or graphing software. If the quadratic equation is easy to graph by hand, it will likely be simpler to use another method to solve the equation.

Granted that you have access to a graph of a given quadratic equation, solving the equation only requires you to find the roots, or the point(s) at which the graph crosses the x-axis. The x-values at these points are the solution(s) to the quadratic equation. For example, given that the graph of a quadratic equation crosses the x-axis at (2, 0), x = 2 is a solution to the quadratic equation.

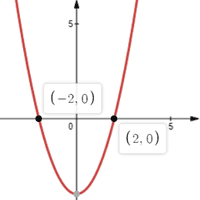
Factoring:

Using factoring to solve a quadratic equation involves first ensuring that the quadratic equation is in standard form. Once it is, factoring the quadratic equation involves some inspection, and possibly some trial and error. The goal of factoring a quadratic equation is to decompose a quadratic equation in standard form into a product of expressions that produces the quadratic equation. If this is possible (it is not always), then we can solve the quadratic equation by setting each expression equal to 0 and solving for x. For example:

x² - x = 6

x² - x - 6 = 0

(x - 3)(x + 2) = 0

x - 3 = 0   or   x + 2 = 0

x = 3   or   x = -2

Thus, x = 3 or x = -2.

This method of solving quadratic equations can be efficient and simple, but not all quadratic equations can be factored in this way, and certain equations can be more complicated to factor.

Completing the square:

Completing the square is a method for solving quadratic equations that involves converting an equation that otherwise cannot be factored, into one that can be factored. Like the quadratic formula (discussed below), completing the square is a method that will work for solving all quadratic equations. However, it is most effective when the coefficient on the x² term is 1, and the coefficient on the x term in the quadratic equation is even. Otherwise, completing the square can be messy, and using the quadratic formula or some other method to solve the equation may be more efficient. Given the standard form of a quadratic equation, ax² + bx + c = 0, the following algorithm can be used to complete the square:

1. If a≠1, divide both sides of the equation by a such that the coefficient on the x² term is 1.
2. Move the constant, c, to the right side of the equation.
3. Find . Recall that ideally, b is and even number.
4. Find and add it to both sides of the equation. Notice that the left-hand side of the equation is now a perfect square.
5. Factor the left-hand side of the equation and simplify the right-hand side.
6. Take the square root of both sides and solve for x.

For example:

Quadratic formula

The quadratic formula is a formula that can be used to solve any quadratic equation. Given a quadratic equation of the form, ax² + bx + c = 0, the quadratic formula is as follows:

where a≠0. To use the quadratic formula, identify a, b, and c, plug them into the formula, then

simplify the expression to find x. Using the previous example from the completing the square section,

x² + 8x - 4 = 0

a = 1, b = 8, and c = -4. Plugging these into the quadratic formula yields:

To reiterate, the quadratic formula can be used to solve any quadratic equation. It is not always the easiest or most efficient method, but it can always be used to solve a quadratic equation.

Discriminant:

The discriminant is the expression in the quadratic formula under the square root sign: b² - 4ac. The discriminant is useful in that we can use it to quickly determine what type of solution(s) the quadratic equation will have. The discriminant can be positive, negative, or equal to 0.

Positive discriminant:

If the discriminant is positive, the quadratic equation will have two real roots. Referencing the above example,

b² - 4ac = 8² - 4(1)(- 4) = 64 + 16 = 80

Since the discriminant is positive, we expect the quadratic equation to have 2 real solutions, as we found that it did, since x = -4±2√5.

Discriminant of 0:

If the discriminant is equal to 0, the quadratic equation will have only one real solution since both solutions of the quadratic equation are the same (the equation has a multiple root as a solution). For example, given the quadratic equation 2x² + 4x + 2 = 0, the discriminant is

b² - 4ac = 4² - 4(2)(2) = 16 - 16 = 0,

and solving the equation using the quadratic formula yields:

Technically, x = -1 + 0 or x = -1 - 0, but adding or subtracting 0 results in the same solution, so there is only 1 solution.

Negative discriminant:

If the discriminant is negative, the quadratic equation has two complex roots. This is because the square root of a negative number is an imaginary number. For example, given the quadratic equation -7x² + x - 2 = 0, the discriminant is:

b² - 4ac = 1² -4(-7)(-2) = 1 - 56 = -55

Since the discriminant is negative, we can expect two complex solutions. Solving the equation using the quadratic formula yields: